\( \DeclareMathOperator{\abs}{abs} \)

Minimize the function \(f(x)=2x^2+y^2\) subject to the constraint \( x^2+y^2=1 \)
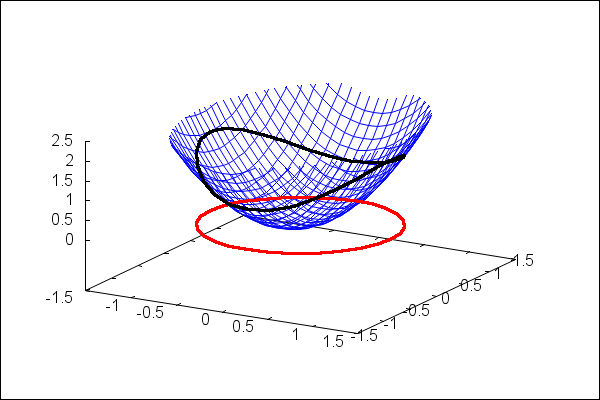
We start with a picture, that shows the surface defined by \(z=f(x,y)\), the constraint \( x^2+y^2=1 \) and the constrained points on the surface

(%i6) load(draw)$
\[\mbox{}\\\mbox{0 errors, 0 warnings}\]
(%i2) fsurf: explicit( 2*x^2 + y^2,x,-1.5,1.5,y,-1.5,1.5);
\[(fsurf)\mathrm{explicit}\left( {{y}^{2}}+2\cdot {{x}^{2}},x,-1.5,1.5,y,-1.5,1.5\right) \]
(%i3) cons: parametric(cos(t),sin(t),0,t,0,2*%pi);
\[(cons)\mathrm{parametric}\left( \mathrm{cos}\left( t\right) ,\mathrm{sin}\left( t\right) ,0,t,0,2\cdot \%pi\right) \]
(%i4) fcons: parametric(cos(t),sin(t),2*cos(t)^2 + sin(t)^2,t,0,2*%pi);
\[(fcons)\mathrm{parametric}\left( \mathrm{cos}\left( t\right) ,\mathrm{sin}\left( t\right) ,{{\mathrm{sin}\left( t\right) }^{2}}+2\cdot {{\mathrm{cos}\left( t\right) }^{2}},t,0,2\cdot \%pi\right) \]
--> wxdraw3d(zrange=[0,2.5],fsurf,line_width=3,color=red,cons,
   color=black,line_width=3,fcons);
\[\mathrm{\tt (\%t5) }\quad \] (Graphics) \[\mathrm{\tt (\%o5) }\quad \]

Now for the Lagrange multiplier calculation:

--> f: 2*x^2+y^2;
\[(f){{y}^{2}}+2\cdot {{x}^{2}}\]
--> g: x^2+y^2;
\[(g){{y}^{2}}+{{x}^{2}}\]
--> solve([diff(f,x)=h*diff(g,x),diff(f,y)=h*diff(g,y),g=1],[x,y,h]);
\[\mathrm{\tt (\%o3) }\quad [[x=1,y=0,h=2],[x=-1,y=0,h=2],[x=0,y=-1,h=1],[x=0,y=1,h=1]]\]

We could also solve for the constraint:

--> s: solve(g=1,y);
\[(s)[y=-\sqrt{1-{{x}^{2}}},y=\sqrt{1-{{x}^{2}}}]\]
--> fx1: ev(f,y=rhs(s[1]));
\[(fx1){{x}^{2}}+1\]
--> fx2: ev(f,y=rhs(s[2]));
\[(fx2){{x}^{2}}+1\]
--> solve(diff(fx1,x),x);
\[\mathrm{\tt (\%o32) }\quad [x=0]\]

And of course we need to consider the endpoints of the interval of possible \(x\) values:  \( x=\pm 1 \), and we see the solution by this method agrees with the Lagrange method above.


Now for a 3D example with Lagrange Multiplier
Minimize the Surface area of a rectangular prism subject to the volume constraint \( xyz=1000 \).

--> A: 2*x*y + 2*y*z+2*z*x;
\[(A)2\cdot y\cdot z+2\cdot x\cdot z+2\cdot x\cdot y\]
--> V: x*y*z;
\[(V)x\cdot y\cdot z\]
--> eq1: diff(A,x)=h*diff(V,x);
\[(eq1)2\cdot z+2\cdot y=h\cdot y\cdot z\]
--> eq2: diff(A,y)=h*diff(V,y);
\[(eq2)2\cdot z+2\cdot x=h\cdot x\cdot z\]
--> eq3: diff(A,z)=h*diff(V,z);
\[(eq3)2\cdot y+2\cdot x=h\cdot x\cdot y\]
--> eq4: V=1000;
\[(eq4)x\cdot y\cdot z=1000\]
--> solve([eq1,eq2,eq3,eq4],[x,y,z,h]);
\[\mathrm{\tt (\%o10) }\quad [[x=10,y=10,z=10,h=\frac{2}{5}]]\]

But now a closely related problem that doesn't work so well with the solver:
Minimize the volume of a rectangular prism subject to the surface area constraint \( 2yz+2xz+2xy=12 \)

--> A: 2*y*z + 2*x*z + 2*x*y;
\[(A)2\cdot y\cdot z+2\cdot x\cdot z+2\cdot x\cdot y\]
--> V(x,y,z):=x*y*z;
\[\mathrm{\tt (\%o14) }\quad \mathrm{V}\left( x,y,z\right) :=x\cdot y\cdot z\]
--> eq1: diff(V(x,y,z),x)=h*diff(A,x);
\[(eq1)y\cdot z=h\cdot \left( 2\cdot z+2\cdot y\right) \]
--> eq2: diff(V(x,y,z),y)=h*diff(A,y);
\[(eq2)x\cdot z=h\cdot \left( 2\cdot z+2\cdot x\right) \]
--> eq3: diff(V(x,y,z),z)=h*diff(A,z);
\[(eq3)x\cdot y=h\cdot \left( 2\cdot y+2\cdot x\right) \]
--> eq4: A=12;
\[(eq4)2\cdot y\cdot z+2\cdot x\cdot z+2\cdot x\cdot y=12\]
--> solve([eq1,eq2,eq3,eq4],[x,y,z,h]);
\[\mathrm{\tt (\%o19) }\quad []\]

Eeek!  Langrange Multipliers didn't yield a solution.
Try substituting the constraint into the function to be optimized:

--> s: solve(A=12,z);
\[(s)[z=-\frac{x\cdot y-6}{y+x}]\]
--> s[1];
\[\mathrm{\tt (\%o21) }\quad z=-\frac{x\cdot y-6}{y+x}\]
--> rhs(s[1]);
\[\mathrm{\tt (\%o22) }\quad -\frac{x\cdot y-6}{y+x}\]
--> Vxy: ev(V,z=rhs(s[1]));
\[(Vxy)-\frac{x\cdot y\cdot \left( x\cdot y-6\right) }{y+x}\]
--> solve([diff(Vxy,x),diff(Vxy,y)],[x,y]);
\[\mathrm{\tt (\%o24) }\quad [[x=0,y=0],[x=-\sqrt{2},y=-\sqrt{2}],[x=\sqrt{2},y=\sqrt{2}],[x=\sqrt{2}\cdot \sqrt{3}\cdot \%i,y=-\sqrt{6}\cdot \%i],[x=-\sqrt{2}\cdot \sqrt{3}\cdot \%i,y=\sqrt{6}\cdot \%i]]\]

If we ignore the unfeasible solutions (non-postive reals and imaginaries), we have \( x=\sqrt{2}, y=\sqrt{2} \)

Created with wxMaxima. The source of this maxima session can be downloaded here.