\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)

Exercise 3, page 809
\[ g(x,y)=4+x^3+y^3-3xy \]

(%i86) g(x,y):=4+x^3+y^3-3*x*y;
\[\tag{\%{}o86}\label{o86} \operatorname{g}\left( x,y\right) :=4+{{x}^{3}}+{{y}^{3}}+\left( -3\right) xy\]
(%i94) gradg: [diff(g(x,y),x),diff(g(x,y),y)];
\[\tag{gradg}\label{gradg}[3{{x}^{2}}-3y,3{{y}^{2}}-3x]\]
(%i96) solve(gradg,[x,y]);
\[\tag{\%{}o96}\label{o96} [[x=-\frac{\sqrt{3}\%{}i+1}{2},y=\frac{\sqrt{3}\%{}i-1}{2}],[x=\frac{\sqrt{3}\%{}i-1}{2},y=-\frac{\sqrt{3}\%{}i+1}{2}],[x=1,y=1],[x=0,y=0]]\]
(%i92) wxdraw3d(
   explicit(g(x,y),x,-1,2,y,-1,2),
      contour_levels={-4,-2,0,2,4,6,7,8},
     contour=base);
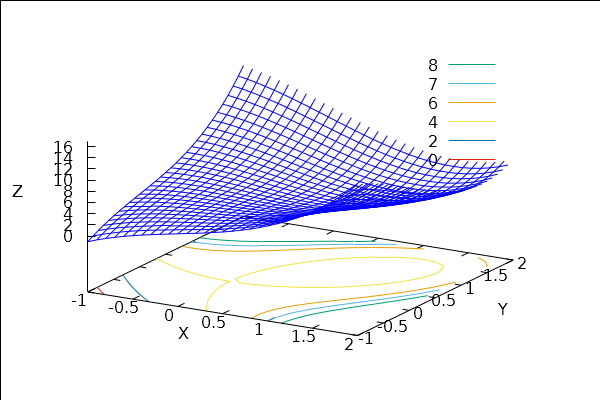
\[\tag{\%{}t92}\label{t92} \] (Graphics)
\[\tag{\%{}o92}\label{o92} \]

We can define the function \( D = f_{xx}f_{yy}-(f_{xy})^2 \) from the second derivative test on page 803:

(%i16) D: diff(g(x,y),x,2)*diff(g(x,y),y,2)-diff(g(x,y),x,1,y,1)^2;
\[\tag{D}\label{D}36xy-9\]

Evaluating \( D \) at each of the (real) critial points shows that there's no local max or min at (0,0),
and there's a local min at (1,1)

(%i22) subst([x=0,y=0],D);
\[\tag{\%{}o22}\label{o22} -9\]
(%i28) ev(D,x=1,y=1);
\[\tag{\%{}o28}\label{o28} 27\]
(%i88) diff(g(x,y),x,2);
\[\tag{\%{}o88}\label{o88} 6x\]
(%i89) ev(%,x=1,y=1);
\[\tag{\%{}o89}\label{o89} 6\]

Example 4, page 804
\[ f(x,y)= 10x^2y-5x^2-4y^2-x^4-2y^4 \]

(%i58) f(x,y):=10*x^2*y-5*x^2-4*y^2-x^4-2*y^4;
\[\tag{\%{}o58}\label{o58} \operatorname{f}\left( x,y\right) :=10{{x}^{2}}y-5{{x}^{2}}+\left( -4\right) \,{{y}^{2}}-{{x}^{4}}+\left( -2\right) \,{{y}^{4}}\]
(%i97) wxdraw3d(
   explicit(f(x,y),x,-3,3,y,-1,3),
      contour_levels=[-4,1,4],
     contour=base);
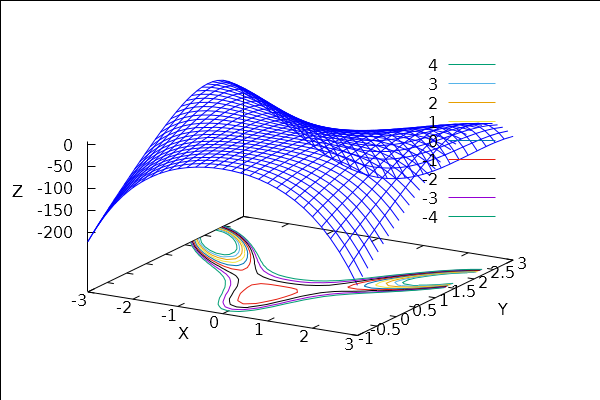
\[\tag{\%{}t97}\label{t97} \] (Graphics)
\[\tag{\%{}o97}\label{o97} \]
(%i59) gradf: [diff(f(x,y),x),diff(f(x,y),y)];
\[\tag{gradf}\label{gradf}[20xy-4{{x}^{3}}-10x,-8{{y}^{3}}-8y+10{{x}^{2}}]\]
(%i62) sol:solve(gradf,[x,y]);
\[\tag{sol}\label{sol}[[x=0,y=-\%{}i],[x=0,y=\%{}i],[x=0,y=0],[x=0.8566569484936832,y=0.6467722289890377],[x=-0.8566569484936832,y=0.6467722289890377],[x=-2.644224422442244,y=1.898384575299635],[x=3.902022956375748\%{}i-5.364619643964067{{10}^{-17}},y=-4.735372218557524{{10}^{-15}}\%{}i-2.545156630416666],[x=-3.902022956375748\%{}i-5.364619643964067{{10}^{-17}},y=-4.735372218557524{{10}^{-15}}\%{}i-2.545156630416666],[x=2.644224422442244,y=1.898384575299635]]\]

What a lot of solutions!  Notice that we can refer to them by their number in the order they are given above, i.e.

(%i64) sol[3];
\[\tag{\%{}o64}\label{o64} [x=0,y=0]\]
--> subst(sol[5],f(x,y));
\[\tag{\%{}o69}\label{o69} -1.484678818966968\]

And we could use the second derivative test to see there is a local max at approximately (2.65,1.90)

(%i105) sol[9];
\[\tag{\%{}o105}\label{o105} [x=2.644224422442244,y=1.898384575299635]\]
(%i70) D:diff(f(x,y),x,2)*diff(f(x,y),y,2)-diff(f(x,y),x,1,y,1)^2;
\[\tag{D}\label{D}\left( 20y-12{{x}^{2}}-10\right) \,\left( -24{{y}^{2}}-8\right) -400{{x}^{2}}\]
(%i103) subst(sol[9],D);
\[\tag{\%{}o103}\label{o103} 2488.718164783891\]
(%i104) subst(sol[9],diff(f(x,y),x,2));
\[\tag{\%{}o104}\label{o104} -55.93538204888755\]
Created with wxMaxima.