\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)

Here we will work on a limit from Multivariable Calculus class:
\[ \lim_{(x,y)\rightarrow (0,0)} \frac{(x-y)^2}{x^2+y^2}.\]
by trying the limit along several paths to see that we don't get the same
value along all paths to the origin

(%i1) f(x,y):=(x-y)^2/(x^2+y^2);
\[\tag{\%{}o1}\label{o1} \operatorname{f}\left( x,y\right) :=\frac{{{\left( x-y\right) }^{2}}}{{{x}^{2}}+{{y}^{2}}}\]

What happens when we try to plug in the origin?

(%i2) f(0,0);
\[\mbox{}\\\mbox{expt: undefined: 0 to a negative exponent.}\mbox{}\\\mbox{\ensuremath{\neq}0: f(x=0,y=0)}\mbox{ -- an error. To debug this try: debugmode(true);}\]

Let's try the limit along the x axis, i.e. y=0:

(%i3) limit(f(x,0),x,0);
\[\tag{\%{}o3}\label{o3} 1\]

And along the y axis, i.e. x=0

(%i4) limit(f(0,y),y,0);
\[\tag{\%{}o4}\label{o4} 1\]

Now along the line y=x:

(%i5) limit(f(x,x),x,0);
\[\tag{\%{}o5}\label{o5} 0\]

And we conclude the limit doesn't exist.
Let's take a look at the graph and notice the behavior

(%i6) wxplot3d(f(x,y),[x,-2,2],[y,-2,2]);
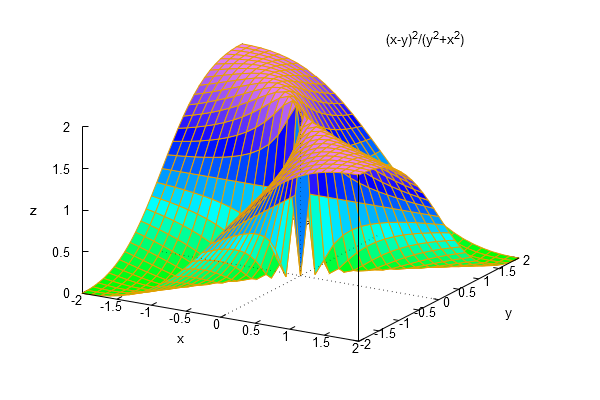
\[\tag{\%{}t6}\label{t6} \] (Graphics)
\[\tag{\%{}o6}\label{o6} \]

This suggests something interest also along the line y=-x:

(%i7) limit(f(x,-x),x,0);
\[\tag{\%{}o7}\label{o7} 2\]
Created with wxMaxima.