\( \DeclareMathOperator{\abs}{abs} \)

For the initial value problem \[    \ddot{x}+2\dot{x}+2x = 2\cos(3t), x(0)=1, \dot{x}(0)=0 \] Find the stead-state solution and estimate a time \( t \) beyond which the absolute value of the transient solution remains less than 1/100.

(%i20) eq: 'diff(x,t,2)+2*'diff(x,t)+2*x = 2*cos(3*t);
\[(eq)\frac{{{d}^{2}}}{d\,{{t}^{2}}}\cdot x+2\cdot \left( \frac{d}{d\,t}\cdot x\right) +2\cdot x=2\cdot \mathrm{cos}\left( 3\cdot t\right) \]
(%i21) gsol: ode2(eq,x,t);
\[(gsol)x=\frac{12\cdot \mathrm{sin}\left( 3\cdot t\right) -14\cdot \mathrm{cos}\left( 3\cdot t\right) }{85}+{{\%e}^{-t}}\cdot \left( \mathit{\%k1}\cdot \mathrm{sin}\left( t\right) +\mathit{\%k2}\cdot \mathrm{cos}\left( t\right) \right) \]
(%i23) psol: ic2(gsol,t=0,x=1,'diff(x,t)=0);
\[(psol)x=\frac{12\cdot \mathrm{sin}\left( 3\cdot t\right) -14\cdot \mathrm{cos}\left( 3\cdot t\right) }{85}+{{\%e}^{-t}}\cdot \left( \frac{63\cdot \mathrm{sin}\left( t\right) }{85}+\frac{99\cdot \mathrm{cos}\left( t\right) }{85}\right) \]
(%i25) wxplot2d(rhs(psol),[t,0,10]);
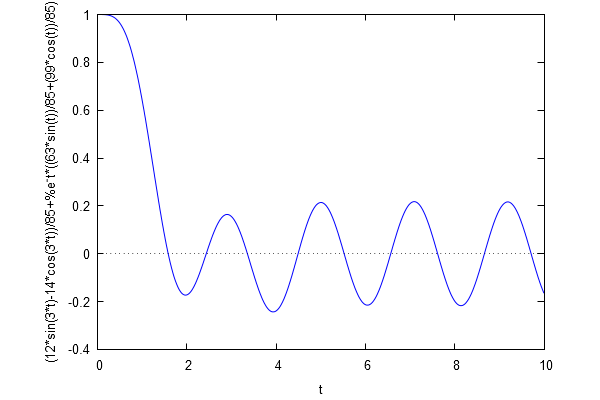\[\mathrm{\tt (\%t25) }\quad \] (Graphics) \[\mathrm{\tt (\%o25) }\quad \]
(%i26) eqH: 'diff(x,t,2)+2*'diff(x,t)+2*x = 0;
\[(eqH)\frac{{{d}^{2}}}{d\,{{t}^{2}}}\cdot x+2\cdot \left( \frac{d}{d\,t}\cdot x\right) +2\cdot x=0\]
(%i27) gsolH: ode2(eqH,x,t);
\[(gsolH)x={{\%e}^{-t}}\cdot \left( \mathit{\%k1}\cdot \mathrm{sin}\left( t\right) +\mathit{\%k2}\cdot \mathrm{cos}\left( t\right) \right) \]

Here's the specific solution:  the general solution of the nonhomogeneous equation minus the general solution of the associated homogeneous equation

(%i35) ssol: rhs(gsol)-rhs(gsolH);
\[(ssol)\frac{12\cdot \mathrm{sin}\left( 3\cdot t\right) -14\cdot \mathrm{cos}\left( 3\cdot t\right) }{85}\]

And so here's the transient solution...the particular solution minus the specific solution

(%i36) tsol: rhs(psol)-ssol;
\[(tsol){{\%e}^{-t}}\cdot \left( \frac{63\cdot \mathrm{sin}\left( t\right) }{85}+\frac{99\cdot \mathrm{cos}\left( t\right) }{85}\right) \]
(%i37) wxplot2d(tsol,[t,0,10]);
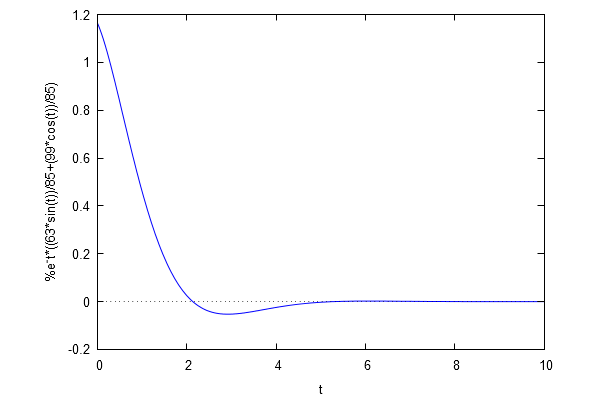\[\mathrm{\tt (\%t37) }\quad \] (Graphics) \[\mathrm{\tt (\%o37) }\quad \]

Now let's hunt and peck for t beyond which the transient solution is less than 0.01 to see that this value of t is something between 4 and 5...certainly t=5 is safe.

(%i49) block( ev(tsol,t=3),float(%%));
\[\mathrm{\tt (\%o49) }\quad -0.0521995134500105\]
(%i50) block( ev(tsol,t=4),float(%%));
\[\mathrm{\tt (\%o50) }\quad -0.02421742809572039\]
(%i51) block( ev(tsol,t=5),float(%%));
\[\mathrm{\tt (\%o51) }\quad -0.002562772032790014\]
(%i52) tsol;
\[\mathrm{\tt (\%o52) }\quad {{\%e}^{-t}}\cdot \left( \frac{63\cdot \mathrm{sin}\left( t\right) }{85}+\frac{99\cdot \mathrm{cos}\left( t\right) }{85}\right) \]

On the other hand, we could make an estimate using the sinusoidal oscillator formula and the fact that \( |\cos(u)| \le 1 \)

(%i66) block(sqrt( (63/85)^2 + (99/85)^2 ),float(%%));
\[\mathrm{\tt (\%o66) }\quad 1.380536979925267\]
(%i67) 0.01/%;
\[\mathrm{\tt (\%o67) }\quad 0.007243558228002943\]
(%i68) -log(%);
\[\mathrm{\tt (\%o68) }\quad 4.927642725359125\]

And finally, we could just use the built-in numerical rootfinder:

(%i78) find_root(abs(tsol)-0.01,t,4,5);
\[\mathrm{\tt (\%o78) }\quad 4.53645430055749\]
Created with wxMaxima. The source of this maxima session can be downloaded here.